
Vecino Mas Cercano
DEFINICION, SUS APLICACIONES Y EJEMPLO...
El algoritmo del vecino más próximo fue, en las ciencias de la computación, uno de los primeros algoritmos utilizados para determinar una solución para el problema del viajante. Este método genera rápidamente un camino corto, pero generalmente no el ideal.
Abajo está la aplicación del algoritmo del vecino más próximo al problema del viajante.
Estos son los pasos del algoritmo:
- elección de un vértice arbitrario respecto al vértice actual.
- descubra la arista de menor peso que ya este conectada al vértice actual y a un vértice no visitado V.
- convierta el vértice actual en V.
- marque V como visitado.
- si todos los vértices del dominio estuvieran visitados, cierre el algoritmo.
- vaya al paso 2.
La secuencia de los vértices visitados es la salida del algoritmo.
El algoritmo del vecino más próximo es fácil de implementar y ejecutar rápidamente, pero algunas veces puede perder rutas más cortas, que son fácilmente notadas con la visión humana, debido a su naturaleza más "ávida". Como norma general, si los últimos pasos del recorrido son comparables en longitud al de los primeros pasos, el recorrido es razonable; si estos son mucho mayores, entonces es probable que existan caminos mucho mejores.
El método del "vecino más cercano"
✔ Disponemos de una tabla resumen de tipo T(n,p)
ALGORITMO
Los ejemplos de entrenamiento son vectores en un espacio característico multidimensional, cada ejemplo está descrito en términos de  atributos considerando
atributos considerando  clases para la clasificación. Los valores de los atributos del
clases para la clasificación. Los valores de los atributos del  -esimo ejemplo (donde
-esimo ejemplo (donde 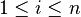 ) se representan por el vector
) se representan por el vector  -dimensional
-dimensional

El espacio es particionado en regiones por localizaciones y etiquetas de los ejemplos de entrenamiento. Un punto en el espacio es asignado a la clase si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la Distancia euclideana.
si esta es la clase más frecuente entre los k ejemplos de entrenamiento más cercano. Generalmente se usa la Distancia euclideana.

La fase de entrenamiento del algoritmo consiste en almacenar los vectores característicos y las etiquetas de las clases de los ejemplos de entrenamiento. En la fase de clasificación, la evaluación del ejemplo (del que no se conoce su clase) es representada por un vector en el espacio característico. Se calcula la distancia entre los vectores almacenados y el nuevo vector, y se seleccionan los  ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
ejemplos más cercanos. El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados.
Este método supone que los vecinos más cercanos nos dan la mejor clasificación y esto se hace utilizando todos los atributos; el problema de dicha suposición es que es posible que se tengan muchos atributos irrelevantes que dominen sobre la clasificación: dos atributos relevantes perderían peso entre otros veinte irrelevantes.
Para corregir el posible sesgo se puede asignar un peso a las distancias de cada atributo, dándole así mayor importancia a los atributos más relevantes. Otra posibilidad consiste en tratar de determinar o ajustar los pesos con ejemplos conocidos de entrenamiento. Finalmente, antes de asignar pesos es recomendable identificar y eliminar los atributos que se consideran irrelevantes.
En síntesis, el método  -nn se resumen en dos algoritmos:
-nn se resumen en dos algoritmos:
Algoritmo de entrenamiento
Para cada ejemplo  ,donde
,donde  , agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.
, agregar el ejemplo a la estructura representando los ejemplos de aprendizaje.
Algoritmo de clasificación
Dado un ejemplar 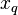 que debe ser clasificado, sean
que debe ser clasificado, sean  los
los  vecinos más cercanos a
vecinos más cercanos a 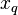 en los ejemplos de aprendizaje, regresar
en los ejemplos de aprendizaje, regresar

donde

el valor 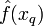 devuelto por el algoritmo como un estimador de
devuelto por el algoritmo como un estimador de  es solo el valor más común de
es solo el valor más común de  entre los
entre los  vecinos más cercanos a
vecinos más cercanos a 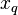 . Si elegimos
. Si elegimos 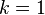 ; entonces el vecino más cercano a
; entonces el vecino más cercano a  determina su valor.
determina su valor.
EJEMPLO 1:
Problema Clásico del Vendedor Viajero - Algoritmo del Vecino más Cercano - Circuito Hamiltoniano

EJEMPLO 2:

|
|
U |
RUTA |
W |
V ´ |
|
INICIO |
- |
C |
0 |
C |
|
|
D |
CD |
3 |
D |
|
|
A |
CDA |
11 |
A |
|
|
B |
CDAB |
16 |
B |
|
FINAL |
C |
CDABC |
23 |
C |
EJEMPLO 3:

|
|
U |
RUTA |
W |
V ´ |
|
INICIO |
- |
A |
0 |
A |
|
|
C |
AC |
3 |
C |
|
|
E |
ACE |
5 |
E |
|
|
D |
ACED |
12 |
D |
|
|
B |
ACEDB |
14 |
B |
|
Final |
A |
ACEDBA |
24 |
A |
EJEMPLO 4:

|
|
U |
RUTA |
W |
V ´ |
|
INICIO |
- |
S |
0 |
S |
|
|
C |
SC |
2 |
C |
|
|
E |
SCE |
10 |
E |
|
|
T |
SCET |
13 |
T |
|
|
D |
SCETD |
19 |
D |
|
|
B |
SCETDB |
24 |
B |
|
|
S |
SCETDBS |
28 |
S |
